Luck: Difference between revisions

Latest revision as of 20:39, 4 September 2025

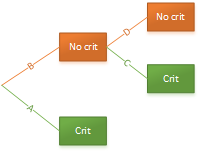
Lucky crit rolls visualized in a tree diagram.

Luck is a mechanic that rolls an outcome or a number in a range twice, with Lucky rolls applying the best result, and Unlucky rolls applying the worst result.

Modifiers that specify Damage or when Damaging and luck refer specifically to damage ranges after any increased/more modifiers (or "tooltip damage range"), not to the base damage of the weapon/skill. These stats do not affect other mechanics like chance to hit/accuracy or critical hit chance.^[1] Additionally, these stats only apply to hit damage, and have no effect on the damage roll of damage over time from damaging ailments, which roll entirely independently of the hit damage's roll.^[2]

Lucky and Unlucky modifiers affecting the same stat or mechanic will cancel each other out.^[3]

Binary Rolls

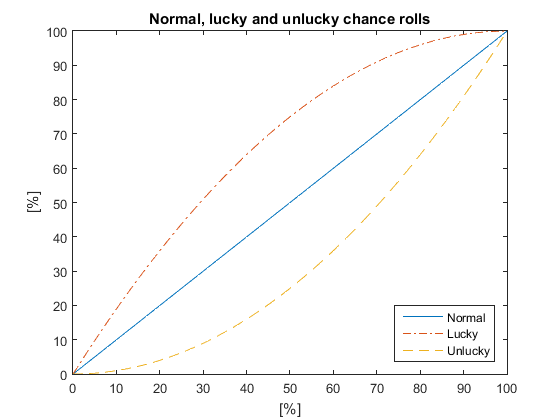
Either roll can make the hit critical, so your critical strike chance on the solid line will be increased to the dash-dotted line on lucky rolls.

A binary roll applies to something with only two choices such as chance of hitting, critical strikes, or chance of blocking. The Lucky or Unlucky chance can be calculated from your original chance with the following formulas:

$\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}Lucky=2\times Chance-{Chance}^{2}$

$\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}Unlucky={Chance}^{2}$

For example, the lucky critical strike chance for a critical strike chance of 40% could be calculated as follows:

$\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}Lucky=2\times 0.4-0.4^{2}=0.8-0.16=0.64$

So a crit chance of 40% will give a lucky crit chance of 64%.

Lucky/unlucky effect on binary rolls
Original chance	Lucky chance	Unlucky chance
10%	19%	1%
25%	43.75%	6.25%
50%	75%	25%
75%	93.75%	56.25%
90%	99%	81%

Note that if a roll has 0% or 100% chance, lucky and unlucky will have no effect.

Damage in a Range

Lucky Damage

Without luck, the average or expected value for a damage roll is $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {min+max}{2}}$ .

A lucky roll has expected value $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {min+2\times max}{3}}$ .

The extra damage luck adds is a sixth of the range, or $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {max-min}{6}}$ .

The average damage is effectively nudged closer toward the max damage, and further from the minimum damage. This means that the larger the range, the more effect luck will have.

Example 1:

You use an attack with a damage range of 600-800, for an average of  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {600+800}{2}}=700$ .
The range, or difference between minimum and maximum, is  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}800-600=200$ .
The bonus damage will be  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {200}{6}}=33.3$  so your new average damage is  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}700+33.3=733.3$ 
To calculate how much more damage this is,  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {733.33}{700}}=1.047$  which means a 4.7% increase.

You can calculate how much more damage lucky will provide as a percentage directly as $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {range}{6\times average}}\times 100\%$ .

Example 2:

You use a spell with a damage range of 100-1000, for an average of  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {100+1000}{2}}=550$  and range of  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}1000-100=900$ .
Adding lucky will give  $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {900}{6\times 550}}=0.273\times 100\%=27.3\%$  more damage.

If your minimum damage is 0 this gives a 33% more multiplier. As the minimum damage increases this scales down to a 0% more multiplier when the minimum damage equals the maximum.

Unlucky Damage

Unlucky damage nudges the damage the opposite way, giving an expected value $\color [rgb]{0.6392156862745098,0.5529411764705883,0.42745098039215684}{\frac {2\times min+max}{3}}$ , which has subtracted a sixth of the range from the original average.

Making damage unlucky will give a less damage multiplier equal to the more damage multiplier that lucky would give, so the same formula as above can be used.

Bifuricate Critical Hits

The Bifuricates Critical Hits causes critical hit chance to be rolled twice. If one of the rolls succeeds, the final hit will be a critical hit. If both rolls succeed, the critical hit damage bonus will be applied twice to the final hit.

When combined with lucky/unlucky critical hit chance, each roll will use the lucky/unlucky values for critical hit chance first.

Related items

Unique items

The following unique items are related to Luck:

Item	Base item		Stats
The Barrow DwellerThe Barrow Dweller Rogue ArmourArmour: 53 Evasion: 43 Movement Speed: -4.0%Requires Level 11, 14 Str, 14 Dex(60-100)% increased Armour and Evasion +(-20--10)% to Fire Resistance +50% to Cold Resistance Damage of Enemies Hitting you is Unlucky while you are on Low Life 50% chance to Avoid Death from HitsIn the mists they dwell, forever hungry, forever cold.	Rogue Armour	11	(60-100)% increased Armour and Evasion +(-20--10)% to Fire Resistance +50% to Cold Resistance Damage of Enemies Hitting you is Unlucky while you are on Low Life 50% chance to Avoid Death from Hits
The Black CatThe Black Cat Grounding CharmLasts 3.00 Seconds Consumes 30 of 40 Charges on use Grants Immunity to ShockRequires Level 32Used when you become Shocked(10–20)% increased Duration Lightning Damage of Enemies Hitting you is Unlucky during effectThe most beloved member of every Brinerot crew is the one that refuses to do any actual work.Used automatically when condition is met. Can only hold charges while in belt. Refill at Wells or by killing monsters.	Grounding Charm	32	Used when you become Shocked(10–20)% increased Duration Lightning Damage of Enemies Hitting you is Unlucky during effect
The BurrowerThe Burrower Topaz RingRequires Level 32+(20-30)% to Lightning Resistance-10% to Cold Resistance +(20-30)% to Lightning Resistance (30-50)% increased Mana Regeneration Rate Lightning Damage of Enemies Hitting you is UnluckyIt coils deeper and deeper It slithers between thoughts It lies beneath the valley It lies in our minds	Topaz Ring	32	+(20-30)% to Lightning Resistance-10% to Cold Resistance +(20-30)% to Lightning Resistance (30-50)% increased Mana Regeneration Rate Lightning Damage of Enemies Hitting you is Unlucky
SvalinnSvalinn Crucible Tower ShieldShield Chance to Block: 26% Armour: 112 Movement Speed: -3.0%Requires Level 72, 66 StrGrants Skill: Raise Shield Grants Skill: Cast on Block(150-200)% increased Armour You take (15-20)% of damage from Blocked hits Block chance is LuckyThe priests found the Great Shield the night it fell to Middengard, but it was the smiths who delved into the secrets it held.	Crucible Tower Shield	72	(150-200)% increased Armour You take (15-20)% of damage from Blocked hits Block chance is Lucky

Related passive skills

Passive skills

The following passive skills are related to Luck: Lua error: Error: Table passive_skills not found..

Ascendancy passive skills

The following Ascendancy passive skills are related to Luck: Lua error: Error: Table passive_skills not found..

Keystone passive skills

The following keystone passive skills are related to Luck: Lua error: Error: Table passive_skills not found..

Related modifiers

The following modifiers are related to Luck: No results found

References

↑ Mark_GGG (May 13, 2013 4:01 AM). "p/c new ring lori's lantern". Path of Exile Forum. Retrieved September 22, 2013.
↑ Confirmed through direct testing by Prohibited Library (community). https://discord.com/channels/991073626721763429/991092346651287623/1165229624595316807
↑ https://www.pathofexile.com/forum/view-thread/3108809/page/1#p24083466

[Lori-1] Mark_GGG (May 13, 2013 4:01 AM). "p/c new ring lori's lantern". Path of Exile Forum. Retrieved September 22, 2013.

[2] Confirmed through direct testing by Prohibited Library (community). https://discord.com/channels/991073626721763429/991092346651287623/1165229624595316807

[3] ttps://www.pathofexile.com/forum/view-thread/3108809/page/1#p24083466

[1]

[2]

[3]

@@ Line 1: / Line 1: @@
 [[File:LuckyCritRolls.png|thumb|right|upright=2|Lucky crit rolls visualized in a [[wikipedia:Tree_diagram_(probability_theory)|tree diagram]].]]
-{{cleanup}}
 '''Luck''' is a mechanic that rolls an outcome or a number in a range twice, with '''Lucky''' rolls applying the ''best'' result, and '''Unlucky''' rolls applying the ''worst'' result.
@@ Line 8: / Line 7: @@
 Lucky and Unlucky modifiers affecting the same stat or mechanic will cancel each other out.<ref>https://www.pathofexile.com/forum/view-thread/3108809/page/1#p24083466</ref>
-==Effectiveness==
+==Binary Rolls==
-With percentage rolls, such as [[critical hit]] chance, lucky/unlucky rolls will be up to a 100% more/less modifier, changing linearly towards 0% as critical chance increases. As for [[receiving damage|damage rolls]], the average damage from the roll will be at up to 33% more or less, when the minimum damage is close to zero, but will have a much weaker effect when the minimum damage is closer to the maximum.
-==Calculations==
-===Binary Rolls===
 [[File:Lucky.PNG|thumb|right|upright=2|Either roll can make the hit critical, so your critical strike chance on the solid line will be increased to the dash-dotted line on lucky rolls.]]
-More specifically, the lucky critical strike chance can be calculated from the following formula:
+A binary roll applies to something with only two choices such as chance of hitting, critical strikes, or chance of blocking. The Lucky or Unlucky chance can be calculated from your original chance with the following formulas:
-{{Math|formula = CritChance_{Lucky} = 2 \times CritChance_{Default} - {CritChance_{Default} } ^ 2 }}
+{{Math|formula = Lucky = 2 \times Chance - {Chance}^2 }}
-For example, the lucky critical strike chance for an default critical strike chance of 40% could be calculated as follows:
+{{Math|formula = Unlucky = {Chance}^2 }}
-{{Math|formula = CritChance_{Lucky} = 2 \times 40\%- 40\% ^ 2 = {{#expr: (2 * 0.4- 0.4 ^ 2) * 100}}\% }}
+For example, the lucky critical strike chance for a critical strike chance of 40% could be calculated as follows:
-It should be noted that these calculations neglect the effect of accuracy on critical strikes.
+{{Math|formula = Lucky = 2 \times 0.4- 0.4 ^ 2 = 0.8 - 0.16 = 0.64}}
-{{blockquote top}}
+So a crit chance of 40% will give a lucky crit chance of 64%.
-<big>'''Derivation of lucky rolls'''</big>
-This is a problem that can be solved with [https://en.wikipedia.org/wiki/Conditional_probability conditional probability].
+{| class="wikitable"
+|+ Lucky/unlucky effect on binary rolls
+|-
+! Original chance!! Lucky chance !! Unlucky chance
+|-
+| 10% || 19% || 1%
+|-
+| 25%|| 43.75% || 6.25%
+|-
+| 50% || 75% || 25%
+|-
+| 75%|| 93.75% || 56.25%
+|-
+| 90% || 99% || 81%
+|}
-Let A be the default critical strike chance on the first roll, then the chance to NOT crit on the first roll is:
+Note that if a roll has 0% or 100% chance, lucky and unlucky will have no effect.
-{{math
+==Damage in a Range==
-|formula = B = 1 - A
+===Lucky Damage===
-|display = block
+Without luck, the average or expected value for a damage roll is {{math|formula=\frac{min+max}{2} }}.
-|ref = {{EquationRef|1}}
-}}
-If the roll failed the die will be cast a second time with the same probabilities. The chance to crit on the second roll is {{EquationNote|1}} multiplied with A:
+A lucky roll has expected value {{math|formula= \frac{min + 2 \times max}{3} }}.
-{{math
+The extra damage luck adds is a sixth of the range, or {{math|formula= \frac{max - min}{6} }}.
-|formula = C = B \times A
-|display = block
-|ref = {{EquationRef|2}}
-}}
-The total probability to get a lucky critical strike is the sum of A and {{EquationNote|2}}.
+The average damage is effectively nudged closer toward the max damage, and further from the minimum damage. This means that the larger the range, the more effect luck will have.
-{{math|formula = \begin{align}
+Example 1:
-CritChance_{Lucky} & = A + C \\
+ You use an attack with a damage range of 600-800, for an average of {{math|formula= \frac{600+800}{2} = 700 }}.
-& = A + B \times A \\
+ The range, or difference between minimum and maximum, is {{math|formula= 800 - 600 = 200 }}.
-& = A + (1 - A) \times A \\
+ The bonus damage will be {{math|formula= \frac{200}{6} = 33.3 }} so your new average damage is {{math|formula=700+33.3 = 733.3 }}
-& = 2 \times A - A^2
+ To calculate how much more damage this is, {{math|formula= \frac{733.33}{700} = 1.047}} which means a 4.7% increase.
-\end{align} }}
-{{blockquote bottom}}
+You can calculate how much more damage lucky will provide as a percentage directly as {{math|formula= \frac{range}{6 \times average} \times 100\% }}.
-===Damage in a Range===
+Example 2:
-Given an integer roll between <var>min</var> and <var>max</var>, the normal expected value is {{math|formula=\frac{min+max}{2} }}.
+ You use a spell with a damage range of 100-1000, for an average of {{math|formula= \frac{100+1000}{2} = 550 }} and range of {{math|formula= 1000-100=900 }}.
+ Adding lucky will give {{math|formula= \frac{900}{6 \times 550} = 0.273 \times 100\% = 27.3\%}} more damage.
-A lucky roll has expected value {{math|formula= \frac{min}{3} + \frac{2*max}{3} + \frac{max-min}{6*(1+max-min)} }}.
+If your minimum damage is 0 this gives a 33% more multiplier. As the minimum damage increases this scales down to a 0% more multiplier when the minimum damage equals the maximum.
-Note that the last term in this is always between 0 and 1/6 and therefore is negligible (it is a byproduct of the fact our uniform variable only takes values over the integers.) This simplifies the formula to {{math|formula=\frac{min+2*max}{3} }}.
+===Unlucky Damage===
+Unlucky damage nudges the damage the opposite way, giving an expected value {{math|formula= \frac{2 \times min + max}{3} }}, which has subtracted a sixth of the range from the original average.
-The average damage is effectively nudged closer toward the max damage, and further from the minimum damage. The damage boost, on average, is a sixth of the difference between minimum and maximum damage.
+Making damage unlucky will give a less damage multiplier equal to the more damage multiplier that lucky would give, so the same formula as above can be used.
-Example 1: You shoot a level 20 {{il|Frost Bomb}}. The minimum damage is 578, and the maximum damage is 867, for an average of 722.5. The difference between minimum and maximum is 289. If the damage is lucky, you get an average 289/6=48.1 extra damage, for a new average damage of 722.5+48.1=770.6 damage. This is a 6.6% damage boost.
+==Bifuricate Critical Hits==
+The {{c|mod|Bifuricates Critical Hits}} causes [[critical hit]] chance to be rolled twice. If one of the rolls succeeds, the final hit will be a critical hit. If both rolls succeed, the critical hit damage bonus will be applied twice to the final hit.
-Example 2: You cast a level 20 {{il|Spark}}. The maximum damage is 1198, and minimum damage is 63, for an average of 630.5. The difference between minimum and maximum is 1135. If the damage is lucky, you get an average 1135/6=189.2 extra damage, for a new average damage of 189.2+630.5=819.6 damage. This is a 30% damage boost.
+When combined with lucky/unlucky critical hit chance, each roll will use the lucky/unlucky values for critical hit chance first.
-How much does lucky improve our expected value - if our minimum damage is 0 then we get a 33% more multiplier. As the minimum damage increases our percentage increase decreases.
 ==Related items==
@@ Line 130: / Line 132: @@
 <ref name="Lori">{{cite web|author=Mark_GGG|date=May 13, 2013 4:01 AM|title=p/c new ring lori's lantern|url=https://www.pathofexile.com/forum/view-thread/377182/page/3#p3349323|publisher=Path of Exile Forum|accessdate= September 22, 2013}}</ref>
 }}
+{{sister|poewiki}}
 [[Category:Game mechanics]]